Simple trend decomposition

Decompose data into trend, cyclical (e.g., daily, annual), and random components using decompose and ts

Usage

decomp(dat_in, ...)

# S3 method for class 'swmpr'
decomp(
  dat_in,
  param,
  type = "additive",
  frequency = "daily",
  start = NULL,
  ...
)

# Default S3 method
decomp(
  dat_in,
  param,
  date_col,
  type = "additive",
  frequency = "daily",
  start = NULL,
  ...
)

Arguments

dat_in: input data object
...: arguments passed to decompose, ts, and other methods
param: chr string of swmpr parameter to decompose
type: chr string of 'additive' or 'multiplicative' indicating the type of decomposition, default 'additive'.
frequency: chr string or numeric vector indicating the periodic component of the input parameter. Only 'daily' or 'annual' are accepted as chr strings. Otherwise a numeric vector specifies the number of observations required for a full cycle of the input parameter. Defaults to 'daily' for a diurnal parameter.
start: numeric vector indicating the starting value for the time series given the frequency. Only required if frequency is numeric. See ts.
date_col: chr string of the name of the date column

Value

Returns a decomposed.ts object

Details

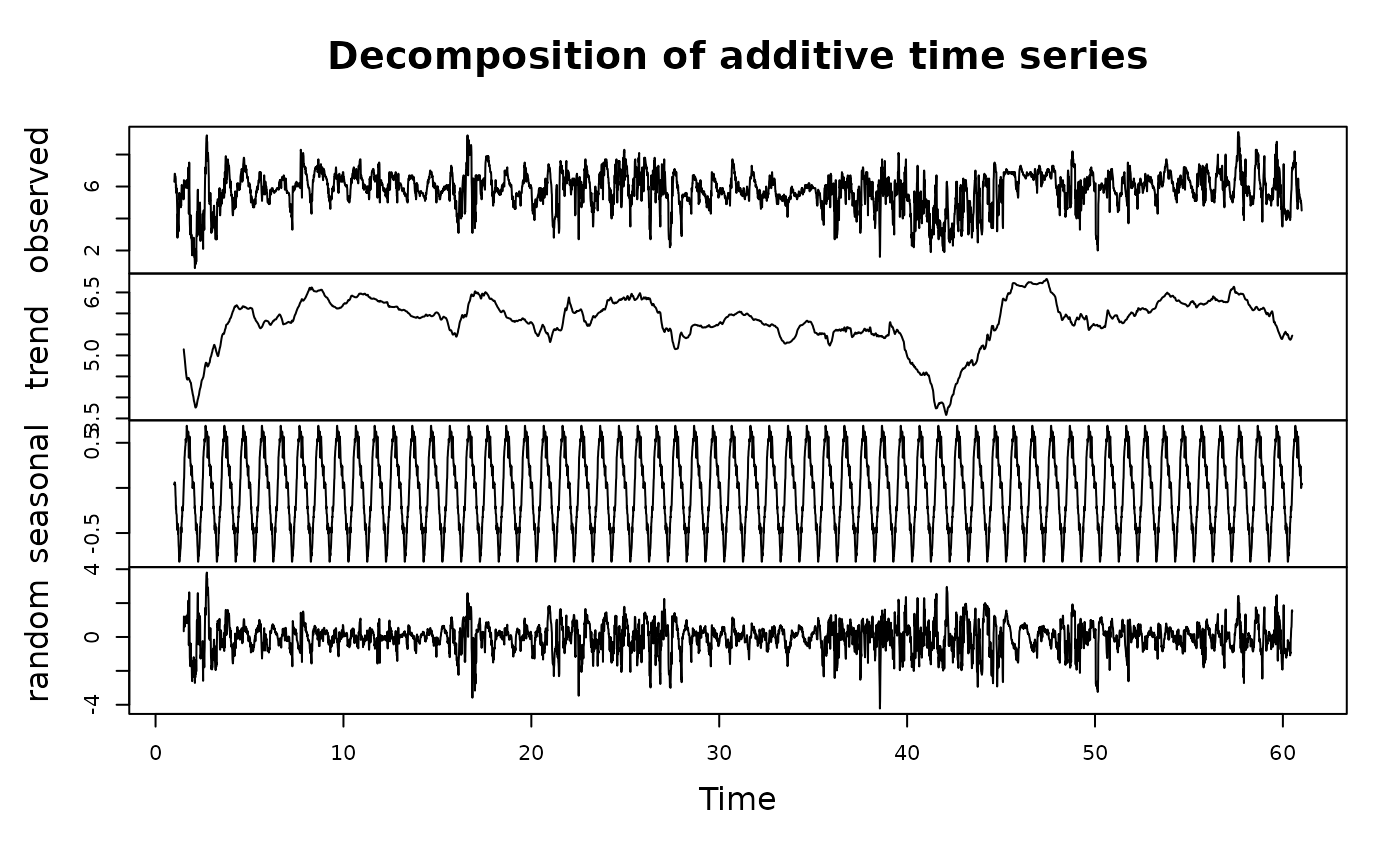
This function is a simple wrapper to the decompose function. The decompose function separates a time series into additive or multiplicative components describing a trend, cyclical variation (e.g., daily or annual), and the remainder. The additive decomposition assumes that the cyclical component of the time series is stationary (i.e., the variance is constant), whereas a multiplicative decomposition accounts for non-stationarity. By default, a moving average with a symmetric window is used to filter the cyclical component. Alternatively, a vector of filter coefficients in reverse time order can be supplied (see decompose).

The decompose function requires a ts object with a specified frequency. The decomp function converts the input swmpr vector to a ts object prior to decompose. This requires an explicit input defining the frequency in the time series required to complete a full period of the parameter. For example, the frequency of a parameter with diurnal periodicity would be 96 if the time step is 15 minutes (24 hours * 60 minutes / 15 minutes). The frequency of a parameter with annual periodicity at a 15 minute time step would be 35040 (365 days * 24 hours * 60 minutes / 15 minutes). For simplicity, chr strings of 'daily' or 'annual' can be supplied in place of numeric values. A starting value of the time series must be supplied in the latter case. Use of the setstep function is required to standardize the time step prior to decomposition.

Note that the decompose function is a relatively simple approach and alternative methods should be investigated if a more sophisticated decomposition is desired.

References

M. Kendall and A. Stuart (1983) The Advanced Theory of Statistics, Vol. 3, Griffin. pp. 410-414.

Examples


## get data
data(apadbwq)
swmp1 <- apadbwq

## subset for daily decomposition
dat <- subset(swmp1, subset = c('2013-07-01 00:00', '2013-07-31 00:00'))

## decomposition and plot
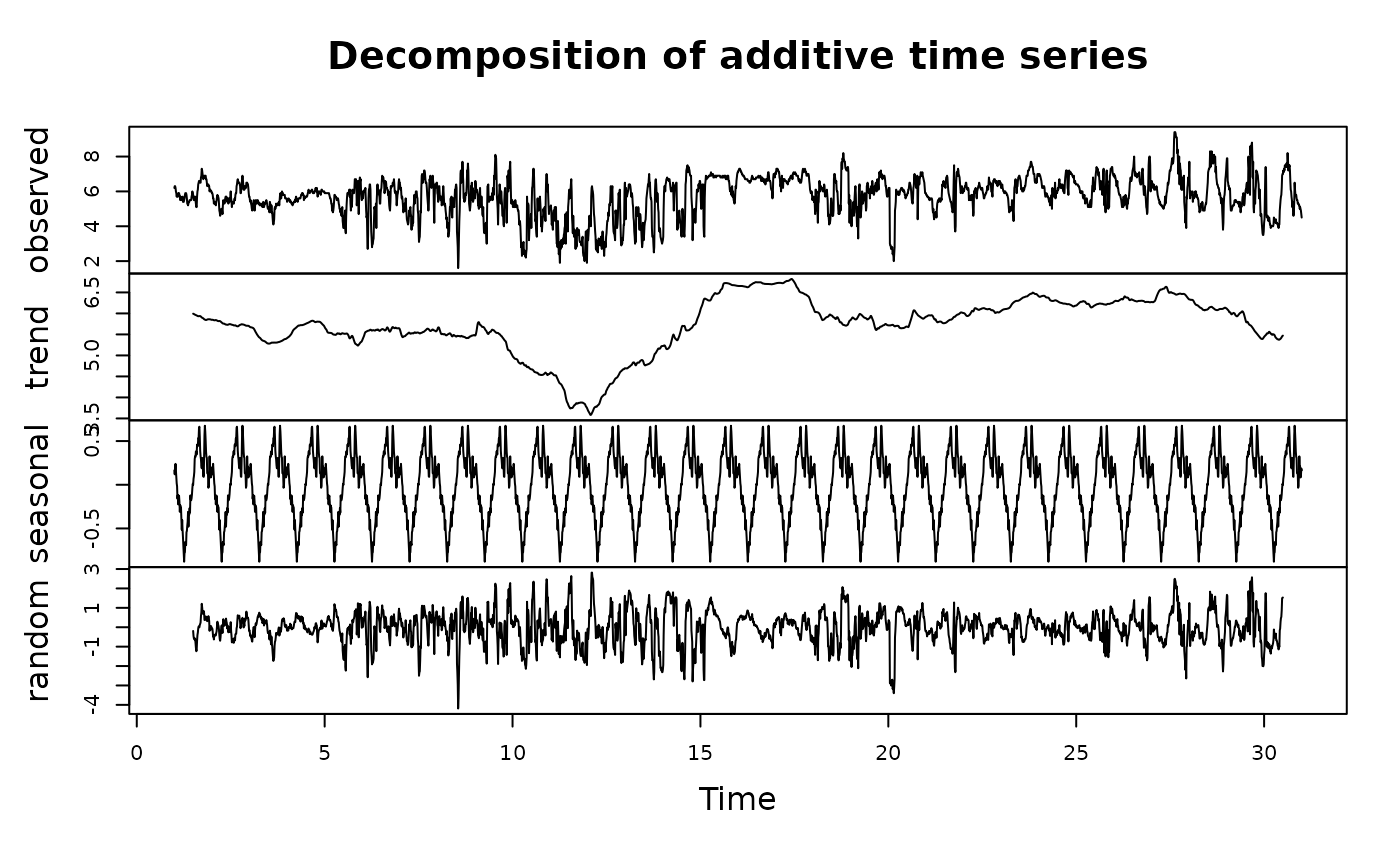
test <- decomp(dat, param = 'do_mgl', frequency = 'daily')
plot(test)


## dealing with missing values
dat <- subset(swmp1, subset = c('2013-06-01 00:00', '2013-07-31 00:00'))

## this returns an error
if (FALSE) { # \dontrun{
test <- decomp(dat, param = 'do_mgl', frequency = 'daily')
} # }

## how many missing values?
sum(is.na(dat$do_mgl))
#> [1] 3

## use na.approx to interpolate missing data
dat <- na.approx(dat, params = 'do_mgl', maxgap = 10)
#> Warning: QAQC columns present, removed in output

## decomposition and plot
test <- decomp(dat, param = 'do_mgl', frequency = 'daily')
plot(test)